In this chunk we will be looking at how we can use vertex functions to create 2-dimensional shapes and animate them to create a fascinating complex-looking animation made from many simple shapes. We will see how we can create lots of 2D hexagons moving in 3D space – a hexagon wave.
We saw in chunk 44 how a shape can be created using lines and vertices, so we will begin by looking at how we can create a hexagon by this method. To do this, we need to work out how to draw each line that makes up the edges of the hexagon shape. This can be done using trigonometry as shown in figure 47.1 below. Trigonometric functions are covered later, so for now you will have to trust is that this works.
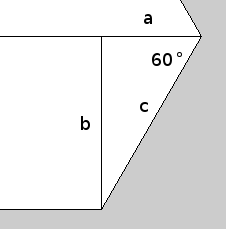
Figure 47.1 The lines needed to draw a hexagon shape
The corresponding code for drawing the hexagon looks like this
// variables for the hexagon sides
float c = 200;
float a = c/2;
float b = sin(radians(60)) * c;
// draw hex shape
beginShape();
vertex(0, b);
vertex(a, 0);
vertex(a + c, 0);
vertex(2 * c, b);
vertex(a + c, 2 * b);
vertex(a + c, 2 * b);
vertex(a, 2 * b);
vertex(0, b);
endShape();
This piece of code will create a shape containing the vertices we define – a line will be drawn between each vertex creating the shape defined between beginShape() and endShape(). If you run this, you will see that a hexagon is drawn similar to that shown in figure 47.2

Figure 47.2 Hexagon shape drawn using vertices
We can make the hexagon slightly more interesting by drawing some lines from each vertex to the centre of the shape. Again, you will have to trust us on the coordinates, but the centre point of the hexagon can be found at point (2*a, b). We already know the points for each vertex as we used them above, so the additional code looks like:
// draw a line from each vertex to the centre of the hexagon
line(0, b, 2 * a, b);
line(a, 0, 2 * a, b);
line(a + c, 0, 2 * a, b);
line(2 * c, b, 2 * a, b);
line(a + c, 2 * b, 2 * a, b);
line(a + c, 2 * b, 2 * a, b);
line(a, 2 * b, 2 * a, b);
Running this along with the code for drawing the hexagon creates a shape like that shown in figure 47.3
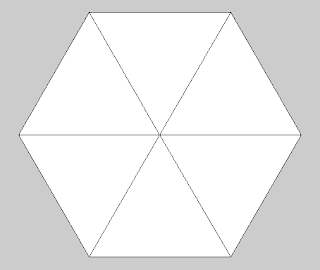
Figure 47.3 Hexagon shape with lines to the centre
Figure 47.3 Hexagon shape with lines to the centre
Now that we have our hexagon, we can start to think about animating it. Processing has rotation functions that allow objects drawn on the screen to be rotated around the x-, y- or z-axis, for example
rotateY(0.1);
will rotate anything drawn after the rotate function by the amount given. In order to do this, either P3D or OPENGL mode needs to be enabled. We will use P3D as it doesn't rely on having an OpenGL-compatible graphics card. This is enabled by specifying it in the size() function eg
size(800, 600, P3D);
However, this will only rotate the hexagon once, where it will appear to be static. To animate a rotating hexagon, we need to use Processing's continuous mode (as seen in chunk 30) and set the background colour each time so the screen is redrawn. We also need to change the rotation each time it is drawn. This is necessary because the rotation is reset each time the draw() function is run so, to give the illusion of rotation, we need to increase the rotation each time the hexagon is drawn. The program so far looks like:
float rotation = 0.1;
void setup() {
// 3D mode
size(900, 500, P3D);
}
void draw() {
background(0);
rotateY(rotation);
// variables for the hexagon sides
float c = 200;
float a = c/2;
float b = sin(radians(60)) * c;
// draw hex shape
beginShape();
vertex(0, b);
vertex(a, 0);
vertex(a + c, 0);
vertex(2 * c, b);
vertex(a + c, 2 * b);
vertex(a + c, 2 * b);
vertex(a, 2 * b);
vertex(0, b);
endShape();
// draw a line from each vertex to the centre of the hexagon
line(0, b, 2 * a, b);
line(a, 0, 2 * a, b);
line(a + c, 0, 2 * a, b);
line(2 * c, b, 2 * a, b);
line(a + c, 2 * b, 2 * a, b);
line(a + c, 2 * b, 2 * a, b);
line(a, 2 * b, 2 * a, b);
rotation += 0.01;
}
Running this will produce a rotating hexagon animation. However, you will see that it rotates from its leftmost point, rather than rotating around the centre of the hexagon. This is because the rotation is taken from the 'origin' of the shape, in this case point (0,b) because we have drawn the shape in relation to that point. To rotate around the centre (which we already have worked out as 2 *a, b) we need to offset the vertices and lines by this point. We will do this by defining points x and y the negative of the centre point ie
float x = -(2 * a);
float y = -b;
Now if x and y are added to the previous vertices coordinates, the hexagon will be drawn in relation to the centre point, giving us
float rotation = 0.1;
void setup() {
// 3D mode
size(900, 500, P3D);
}
void draw() {
// draw in the middle of the screen
translate(width/2,height/2); // 1
// reset the page with a background colour
background(0);
// rotate around the Y axis
rotateY(rotation);
// variables for the hexagon sides
float c = 200;
float a = c/2;
float b = sin(radians(60)) * c;
// define the centre variables
float x = -(2 * a);
float y = -b;
// draw hex shape
beginShape();
vertex(x, y + b);
vertex(x + a, y);
vertex(x + a + c, y);
vertex(x + (2 * c), y + b);
vertex(x + a + c, y + (2 * b));
vertex(x + a + c, y + (2 * b));
vertex(x + a, y + (2 * b));
vertex(x, y + b);
endShape();
// draw a line from each vertex to the centre of the hexagon
line(x, y + b, x + (2 * a), y + b);
line(x + a, y, x + (2 * a), y + b);
line(x + a + c, y, x + (2 * a), y + b);
line(x + (2 * c), y + b, x + (2 * a), y + b);
line(x + a + c, y + (2 * b), x + (2 * a), y + b);
line(x + a + c, y + (2 * b), x + (2 * a), y + b);
line(x + a, y + (2 * b), x + (2 * a), y + b);
// increase rotation
rotation += 0.01;
}
Running this will now display our hexagon rotating around its centre point – a nice little animation, although not particularly exciting. We needed to add an extra line of code here to display the hexagon properly, in the middle of the screen (labelled //1 in the code above). The translate function in Processing moves the origin of the graphics following the translate() to the position given in the function. In our case we are telling Processing to draw the hexagon and lines in the centre of the screen, shown by (width/2,height/2)
Figure 47.4 Centred rotating hexagon
To make this more exciting, we will now replicate the hexagon to produce lots of hexagons. This could be done using arrays of vertex points representing the vertices of each hexagon, but this would get complicated very quickly. Fortunately, Processing has a better way of reproducing graphics that we can use to just keep drawing the same hexagon but display many versions of it – the matrix stack.
We won't explain exactly how the matrix stack works, except to say that it rests behind the way Processing works in order to display graphics using a stack (like a stack of coins, you can only get to the top coin so have to work down the stack of coins to get to the bottom). By getting access to the matrix (using pushMatrix()), we can alter the way graphics are displayed, then put the matrix back again (using popMatrix()) for Processing to display. If we were to alter the graphics by displaying a hexagon and moving it using the translate() function, many times, we would give the appearance of lots of hexagons without needing to maintain where each one should be displayed – this can be a very powerful feature, which we will now demonstrate.
float rotation = 0.1;
// the number of hexagons
int xCount = 10; //1
// the length of 1 hexagon side
int sideLength = 50; //2
void setup() {
// 3D mode
size(900, 500, P3D);
}
void draw() {
// reset the page with a background colour
background(0);
// loop the number of times specified
for (int i = 0; i < xCount; i ++) { //3
// push the matrix
pushMatrix(); //4
// translate the hexagon to one sise
translate((sideLength * 2) * i, height/2); //5
// rotate around the Y axis
rotateY(rotation);
// variables for the hexagon sides
float c = sideLength;
float a = c/2;
float b = sin(radians(60)) * c;
// define the centre variables
float x = -(2 * a);
float y = -b;
// draw hex shape
beginShape();
vertex(x, y + b);
vertex(x + a, y);
vertex(x + a + c, y);
vertex(x + (2 * c), y + b);
vertex(x + a + c, y + (2 * b));
vertex(x + a + c, y + (2 * b));
vertex(x + a, y + (2 * b));
vertex(x, y + b);
endShape();
// draw a line from each vertex to the centre of the hexagon
line(x, y + b, x + (2 * a), y + b);
line(x + a, y, x + (2 * a), y + b);
line(x + a + c, y, x + (2 * a), y + b);
line(x + (2 * c), y + b, x + (2 * a), y + b);
line(x + a + c, y + (2 * b), x + (2 * a), y + b);
line(x + a + c, y + (2 * b), x + (2 * a), y + b);
line(x + a, y + (2 * b), x + (2 * a), y + b);
popMatrix(); //6
}
// increase rotation
rotation += 0.01;
}
If you run the above code, you will see that we have created ten hexagons without storing where each one is being displayed at all! Each one is just a copy of the same hexagon, displayed in a different place and rotated.

Figure 47.5 Ten hexagons created using the translate() function
The changes we made to do this are very small, using just 6 lines of additional code (numbered above). In lines //1 and //2 we have created variables to control the number of hexagons and the size of each side of the hexagon. We use a for statement in line //3 to loop the number of times defined in the xCount variable, creating a hexagon each time, translating each one (line //5) by shifting each to the side. Lines //4 and //6 are the matrix methods that enable this to work. It would be easy, using this method, to fill the screen with hexagons by translating more of them using a further for statement, for example
for (int i = 0; i <= xCount; i++) {
// translate each hexagon to the side
translate(10 * i, 0, 0);
// for every column of hexagons
for (int j = 0; j <= yCount; j++) {
translate((sideLength * 2), (sideLength * 2), 0);
In order to tidy up our hexagon drawing code and prevent duplication (you will see why later), we can also move this into a function so that we can call the function each time we want to draw one. We have called this function drawHexagon() and created a function for drawing the lines called drawLines(),
We can now start to make our animation really exciting by making the hexagons more wave-like. If we define a maximum and minimum number of hexagons, we can increase and decrease them with each run of the draw() function, like a tide. We will need several variables for this
// maximum number of hexagons on the Y and X axes
int maxXCount = 20;
int maxYCount = 20;
// minimum number of hexagons on the Y anc X axis
int minXCount = 1;
int minYCount = 1;
// current number of hexagons
int xCount = minXCount;
int yCount = minYCount;
// whether the number of hexagons is increasing
boolean xIncreasing = true;
boolean yIncreasing = true;
Each time the draw() function is run, we will either increase or decrease the number of hexagons depending on whether the current number of hexagons is less than the minimum number or greater than the maximum. These will be controlled using some functions that will determine whether they should be increasing or not and altering the current count (xCount and yCount) accordingly.
/**
* determine the direction of the hexagons
*/
void determineDirection() {
// if the x-axis is increasing
if (xIncreasing) {
// increase the number of hexagons
xCount++;
}
// otherwise decrese them
else {
xCount--;
}
// if the y-axis is increasing
if (yIncreasing) {
// increase the number of hexagons
yCount++;
}
// otherwise decrease them
else {
yCount--;
}
}
/**
*Determine whether the number of hexagons should be increasing or not
*/
void determineIncreasingStatus() {
// if the number of hexagons on the x-axis is greater than the maximum
if (xCount > maxXCount) {
// set to decrease
xIncreasing = false;
}
// if the number of hexagons on the x-axis is greater than the maximum
if (yCount > maxYCount) {
// set to decrease
yIncreasing = false;
}
// if the number of hexagons on the x-axis is less than the minimum
if (xCount < minXCount) {
// set to increase
xIncreasing = true;
}
// if the number of hexagons on the y-axis is less than the minimum
if (yCount < minYCount) {
// set to increase
yIncreasing = true;
}
}
If we call these functions from the draw() function, we will have created our wave effect – the hexagons will increase until they reach the maximum, then decrease again. Our draw() function now looks like:
void draw() {
// determine how many hexagons there should be
determineDirection();
// reset the page with a background colour
background(0);
// loop for the number of hexagons on the x-axis
for (int i = 0; i <= xCount; i++) {
// push the matrix
pushMatrix();
// translate each hexagon to the side
translate((sideLength * 2) * i, 0, 0);
// loop for the number of hexagons on the y-axis
for (int j = 0; j <= yCount; j++) {
translate((sideLength * 2), (sideLength * 2), 0);
// rotate around the Y axis
rotateY(rotation);
// draw the hexagon
drawHexagon();
// draw the lines
drawLines();
}
popMatrix();
}
// increase rotation
rotation += 0.01;
// determine if the hexagons should be increasing in number
determineIncreasingStatus();
}
Running our code now will produce an increasing, then decreasing, number of hexagons, all rotating at slightly different points, as shown in figure 47.6
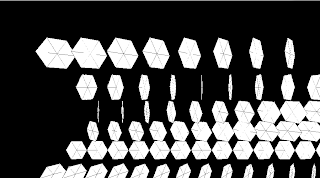
Figure 47.6 Wave of hexagons
You will notice, however, that is rather fast and not altogether wave like! We can sort this out by slowing down the animation using Processing's frameRate() function. This controls how fast the animation is displayed – the default is 30, but 8 seems to produce the best effect for this animation. Adding the following into the setUp() function should produce the desired result
frameRate(8);
Now all that remains is make our animation more fun! We can make a really good wave effect by translating the whole screen to skew the viewing angle, increasing the number of hexagons and reducing their size. All we need to do is increase the maxXCount and maxYCount variables to 80, decrease the sideLength variable to 5 and add the following line to the to the top of the draw() function
rotateX(1.0);
This line will rotate the entire viewing angle of the screen. Running it now will display an interesting wave-like effect – the hexagons will seem to 'wash' in from the left of the screen in a wave formation, then wash out again.

Figure 47.7 Hexagon wave
That is essentially the core of our line-based animation. We have created an animation of rotating hexagons that exhibit a wave-like formation by rotating the screen and drawing a differing number of hexagons each time the draw() function is run. Different animations can be obtained by altering the program a little, for example adding colour (explored later in the book) or creating multiple waves. This is where moving the hexagon-drawing code into a function can prove useful. We have created two waves by moving some of the draw() code into a drawLeftWave() which is called from the draw() function so that we can also create a drawRightWave() function that starts from the top-right corner by reversing the x-axis attribute in the translate() function. The code for this is below – try it and watch what happens when the two waves meet each other. You can alter it however you want with just minor changes and watch the effects
// the rotation of the hexagons
float rotation;
// maximum number of hexagons on the Y and X axes
int maxXCount;
int maxYCount;
// minimum number of hexagons on the Y anc X axis
int minXCount;
int minYCount;
// current number of hexagons
int xCount;
int yCount;
// whether the number of hexagons are increasing
boolean xIncreasing;
boolean yIncreasing;
// variables for the hexagon sides
float a;
float b;
float c;
// variables for the centre of a hexagon
float x;
float y;
// the length of a single hexagon side
int sideLength = 5;
/**
* setup and initialise the sketch
*/
void setup() {
// 3D mode
size(900, 500, P3D);
// calculate the sides of the hexagon
c = sideLength;
a = c / 2;
b = sin(radians(60)) * c;
// origin coordinates for the hexagon
x = -(2 * a);
y = -b;
// initialise the maximum number of hexagons
maxXCount = 80;
maxYCount = 80;
// initialise the minimum number of hexagons
minXCount = 1;
minYCount = 1;
// initialise the starting number of hexagons as the minimum number
xCount = minXCount;
yCount = minYCount;
// start by increasing the number of hexagons
xIncreasing = true;
yIncreasing = true;
// start by rotating anti-clockwise
rotation = -PI;
// make the frame rate quite low
frameRate(8);
}
/**
* Draw the screen in repeat mode
*/
void draw() {
// determine how many hexagons there should be
determineDirection();
// reset the page with a background colour
background(0);
// rotate the entire display
rotateX(1.0);
// draw the left wave of hxagons
drawLeftWave();
// draw the right wave of hexagons
drawRightWave();
// increase rotation
rotation += 0.01;
// determine whether the hexagons should be increasing or decreasing
determineIncreasingStatus();
}
/**
* Draw the left wave of hexagons
*/
void drawLeftWave() {
// fill the hexagons with yellow and alpha value
fill(238, 238, 0, 150);
// for row of hexagons
for (int i = 0; i <= xCount; i++) {
// push the matrix
pushMatrix();
// translate each hexagon to the side
translate((sideLength * 2) * i, 0, 0);
// for every column of hexagons
for (int j = 0; j <= yCount; j++) {
// translate each forward and sideways
translate((sideLength * 2), (sideLength * 2), 0);
// rotate around the y axis
rotateY(rotation);
// draw a hexagon
drawHexagon();
// draw the interior lines
drawLines();
}
popMatrix();
}
}
/**
* Draw the right wave of hexagons
*/
void drawRightWave() {
// fill the hexagons with red and alpha value
fill(165, 42, 42, 150);
// for row of hexagons
for (int i = 0; i <= xCount; i++) {
// push the matrix
pushMatrix();
// translate each hexagon to the side
translate(width - (sideLength * 2) * i, 0, 0);
// for every column of hexagons
for (int j = 0; j <= yCount; j++) {
// translate each forward and sideways
translate((sideLength * 2), (sideLength * 2), 0);
// rotate around the y axis
rotateY(rotation);
// draw a hexagon
drawHexagon();
// draw the interior lines
drawLines();
}
popMatrix();
}
}
/**
* determine the direction of the hexagons
*/
void determineDirection() {
// if the x-axis is increasing
if (xIncreasing) {
// increase the number of hexagons
xCount++;
}
// otherwise decrese them
else {
xCount--;
}
// if the y-axis is increasing
if (yIncreasing) {
// increase the number of hexagons
yCount++;
}
// otherwise decrese them
else {
yCount--;
}
}
/**
*Determine whether the number of hexagons should be increasing or not
*/
void determineIncreasingStatus() {
// if the number of hexagons on the x-axis is greater than the maximum
if (xCount > maxXCount) {
// set to decrease
xIncreasing = false;
}
// if the number of hexagons on the x-axis is greater than the maximum
if (yCount > maxYCount) {
// set to decrease
yIncreasing = false;
}
// if the number of hexagons on the x-axis is less than the minimum
if (xCount < minXCount) {
// set to increase
xIncreasing = true;
}
// if the number of hexagons on the y-axis is less than the minimum
if (yCount < minYCount) {
// set to increase
yIncreasing = true;
}
}
/**
* Draw a hexagon
*/
void drawHexagon() {
// draw hex shape
beginShape();
vertex(x, y + b);
vertex(x + a, y);
vertex(x + a + c, y);
vertex(x + (2 * c), y + b);
vertex(x + a + c, y + (2 * b));
vertex(x + a + c, y + (2 * b));
vertex(x + a, y + (2 * b));
vertex(x, y + b);
endShape();
}
/**
* Draw the interior lines of the hexagon
*/
void drawLines() {
// draw a line from each vertex to the centre of the hexago
line(x, y + b, x + (2 * a), y + b);
line(x + a, y, x + (2 * a), y + b);
line(x + a + c, y, x + (2 * a), y + b);
line(x + (2 * c), y + b, x + (2 * a), y + b);
line(x + a + c, y + (2 * b), x + (2 * a), y + b);
line(x + a + c, y + (2 * b), x + (2 * a), y + b);
line(x + a, y + (2 * b), x + (2 * a), y + b);
}

Figure 47.8 Hexagon waves
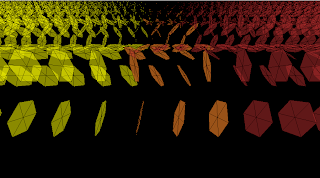
Figure 47.9 Hexagons waves crashing into each other
