First 500-1000 Words-ish (Draft)

Putting it all together 2
In this chunk we will be looking at how we can use vertex functions to create 2-dimensional shapes and animate them to create a fascinating complex-looking animation made from many simple shapes. We will see how we can create lots of 2D hexagons moving in 3D space – a hexagon wave.
We saw in chunk 44 how a shape can be created using lines and vertices, so we will begin by looking at how we can create a hexagon by this method. To do this, we need to work out how to draw each line that makes up the edges of the hexagon shape. This can be done using trigonometry as shown in figure 47.1 below. Trigonometric functions are covered later, so for now you will have to trust is that this works.

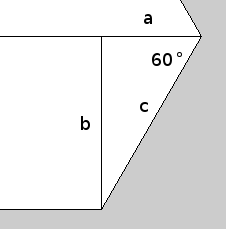
Figure 47.1 The lines needed to draw a hexagon shape

The corresponding code for drawing the hexagon looks like this

// variables for the hexagon sides
float c = 200;
float a = c/2;
float b = sin(radians(60)) * c;
// draw hex shape
beginShape();
vertex(0, b);
vertex(a, 0);
vertex(a + c, 0);
vertex(2 * c, b);
vertex(a + c, 2 * b);
vertex(a + c, 2 * b);
vertex(a, 2 * b);
vertex(0, b);
endShape();

This piece of code will create a shape containing the vertices we define – a line will be drawn between each vertex creating the shape defined between beginShape() and endShape(). If you run this, you will see that a hexagon is drawn similar to that shown in figure 47.2

Figure 47.2 Hexagon shape drawn using vertices

We can make the hexagon slightly more interesting by drawing some lines from each vertex to the centre of the shape. Again, you will have to trust us on the coordinates, but the centre point of the hexagon can be found at point (2*a, b). We already know the points for each vertex as we used them above, so the additional code looks like:

// draw a line from each vertex to the centre of the hexagon
line(0, b, 2 * a, b);
line(a, 0, 2 * a, b);
line(a + c, 0, 2 * a, b);
line(2 * c, b, 2 * a, b);
line(a + c, 2 * b, 2 * a, b);
line(a + c, 2 * b, 2 * a, b);
line(a, 2 * b, 2 * a, b);

Running this along with the code for drawing the hexagon creates a shape like that shown in figure 47.3

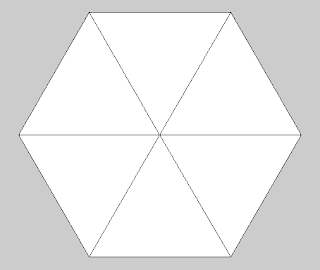
Figure 47.3 Hexagon shape with lines to the centre

Now that we have our hexagon, we can start to think about animating it. Processing has rotation functions that allow objects drawn on the screen to be rotated around the x-, y- or z-axis, for example
rotateY(0.1);
will rotate anything drawn after the rotate function by the amount given. In order to do this, either P3D or OPENGL mode needs to be enabled. We will use P3D as it doesn't rely on having an OpenGL-compatible graphics card. This is enabled by specifying it in the size() function eg

 size(800, 600, P3D);

However, this will only rotate the hexagon once, where it will appear to be static. To animate a rotating hexagon, we need to use Processing's continuous mode (as seen in chunk 30) and set the background colour each time so the screen is redrawn. We also need to change the rotation each time it is drawn. This is necessary because the rotation is reset each time the draw() function is run so, to give the illusion of rotation, we need to increase the rotation each time the hexagon is drawn. The program so far looks like:

float rotation = 0.1;

void setup() {
  // 3D mode
  size(900, 500, P3D);
}

void draw() {
  background(0);
  rotateY(rotation);

  // variables for the hexagon sides
  float c = 200;
  float a = c/2;
  float b = sin(radians(60)) * c;
  // draw hex shape
  beginShape();
  vertex(0, b);
  vertex(a, 0);
  vertex(a + c, 0);
  vertex(2 * c, b);
  vertex(a + c, 2 * b);
  vertex(a + c, 2 * b);
  vertex(a, 2 * b);
  vertex(0, b);
  endShape();

  // draw a line from each vertex to the centre of the hexagon
  line(0, b, 2 * a, b);
  line(a, 0, 2 * a, b);
  line(a + c, 0, 2 * a, b);
  line(2 * c, b, 2 * a, b);
  line(a + c, 2 * b, 2 * a, b);
  line(a + c, 2 * b, 2 * a, b);
  line(a, 2 * b, 2 * a, b);

  rotation += 0.01;

}

Running this will produce a rotating hexagon animation. However, you will see that it rotates from its leftmost point, rather than rotating around the centre of the hexagon. This is because the rotation is taken from the 'origin' of the shape, in this case point (0,b) because we have drawn the shape in relation to that point. To rotate around the centre (which we already have worked out as 2 *a, b) we need to offset the vertices and lines by this point. We will do this by defining points x and y the negative of the centre point ie

 float x = -(2 * a);
 float y = -b;

Now if x and y are added to the previous vertices coordinates, the hexagon will be drawn in relation to the centre point, giving us

float rotation = 0.1;

void setup() {
  // 3D mode
  size(900, 500, P3D);
}

void draw() {
  // draw in the middle of the screen
  translate(width/2,height/2); // 1
  // reset the page with a background colour
  background(0);
  // rotate around the Y axis
  rotateY(rotation);

  // variables for the hexagon sides
  float c = 200;
  float a = c/2;
  float b = sin(radians(60)) * c;
  // define the centre variables
  float x = -(2 * a);
  float y = -b;
  // draw hex shape
  beginShape();
  vertex(x, y + b);
  vertex(x + a, y);
  vertex(x + a + c, y);
  vertex(x + (2 * c), y + b);
  vertex(x + a + c, y + (2 * b));
  vertex(x + a + c, y + (2 * b));
  vertex(x + a, y + (2 * b));
  vertex(x, y + b);
  endShape();

  // draw a line from each vertex to the centre of the hexagon
  line(x, y + b, x + (2 * a), y + b);
  line(x + a, y, x + (2 * a), y + b);
  line(x + a + c, y, x + (2 * a), y + b);
  line(x + (2 * c), y + b, x + (2 * a), y + b);
  line(x + a + c, y + (2 * b), x + (2 * a), y + b);
  line(x + a + c, y + (2 * b), x + (2 * a), y + b);
  line(x + a, y + (2 * b), x + (2 * a), y + b);
  // increase rotation
  rotation += 0.01;

}

Running this will now display our hexagon rotating around its centre point – a nice little animation, although not particularly exciting. We needed to add an extra line of code here to display the hexagon properly, in the middle of the screen (labelled //1 in the code above). The translate function in Processing moves the origin of the graphics following the translate() to the position given in the function. In our case we are telling Processing to draw the hexagon and lines in the centre of the screen, shown by (width/2,height/2).